Nuevamente saludándote, ahora con el tema de calculo de longitudes y superficies del mapa, plano o croquis.
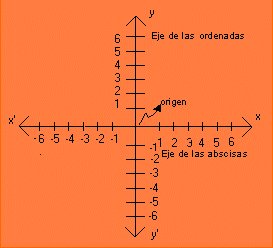
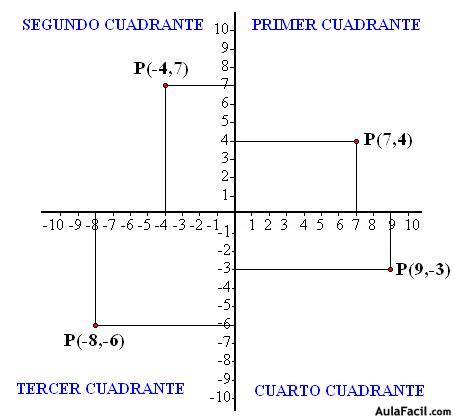
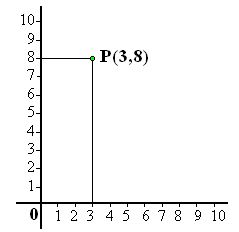
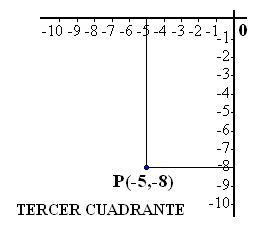
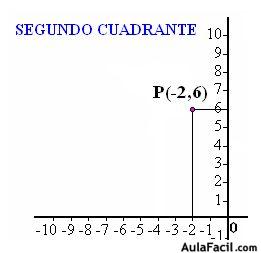
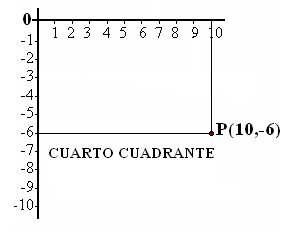
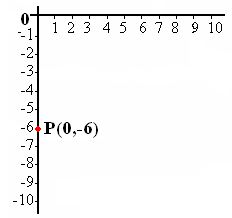
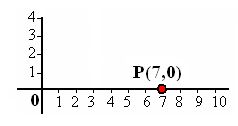
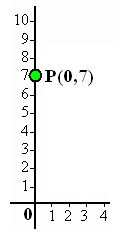
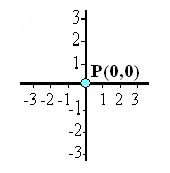
Resumiendo un poco lo que viste en el tema anterior, ya podemos entender la diferencia entre relación y función, también podemos identificar puntos en el plano cartesiano, y características de las coordenadas de un punto cuando se encuentran en cualquiera de los cuatro cuadrantes del plano cartesiano.
Ahora, basándonos en la ubicación de dos puntos determinaremos la distancia entre esos dos puntos.
Distancia entre dos puntos:
Cuando dos
puntos están situados en un eje numérico es muy simple calcular la distancia
entre ellos.
En un sistema
coordenado unidimensional, la distancia dirigida entre los puntos P1(x1)
y P2(x2) se
obtiene restando a la coordenada del punto final la coordenada del punto
inicial.
P1P2
= x2 – x1 P2P1
= x1 – x2
Así, por ejemplo:
A(-2) y B(3)
La distancia
dirigida de A a B es 5
AB = 3 – (-2) = 3 + 2 = 5
La distancia
dirigida de B a A es -5
BA = - 2 – 3 = -5
Cuando no se
considera el sentido, se habla simplemente de distancia entre los puntos.
En un sistema coordenado bidimensional la
distancia entre dos puntos P1(x1,y1) y P2(x2,y2)
se
Obtiene con la fórmula:

Anexo video
ÁREA DE UN TRIÁNGULO EN FUNCIÓN DE SUS COORDENADAS:
Es posible
determinar el área de un polígono
situado en un plano cartesiano, aplicando
un
Procedimiento sencillo. Éste se basa en la fórmula para
hallar el área de un triangulo, también llamado por determinantes.
El área del triángulo
con vértices P1(x1,y1), P2(x2,y2)
y P3(x3,y3), es igual al valor absoluto de:
A
= ½ x2 y2
X3 y3
X1 y1
Ejemplo:
Calcular el área
del triángulo cuyos vértices son: A(-1,3), B(6,4) y C(-2,-5), es igual al valor
A = ½ 6
4
-2 -5
-1
3
Por tanto, A = ½ | -55 | = ( ½
)(55) = 27.5 u2
Anexo video
PENDIENTE DE UNA
RECTA:
La pendiente m
de una recta que pasa por dos puntos dados P1(x1,y1)
y P2(x2,y2) es igual a la diferencia de las
ordenadas dividida entre la diferencia de las abscisas tomadas en el mismo
orden;
es decir y2
– y1
m = -----------
x2 – x1
La pendiente de una recta se define como la tangente de su ángulo de
inclinación. Una recta
que se inclina hacia la derecha tiene una pendiente
positiva, ya que la inclinación es un ángulo agudo.
Las pendientes
de las rectas que se inclinan hacia la izquierda son negativas y forman un
Ángulo obtuso con respecto al eje de las x ,s.
Para obtener la
inclinación de una recta aplicamos la formula siguiente:
m = tan ø
por lo tanto: ø = tan
-1
 |
Anexo video
Angulo entre dos rectas en el plano:
Una de las formas mas comunes y simples de poder encontrar el angulo que forman dos rectas es la relación que existe entre sus pendientes.
por ejemplo, me piden que determine el angulo formado por la recta r cuya pendiente es de -2 y la recta s cuya pendiente es de 0.5
El primer criterio que debemos realizar es identificar las pendientes ( m1
y m2 ) y para esto nos piden que seleccionemos las pendientes en sentido contrario a las maesillas del reloj.
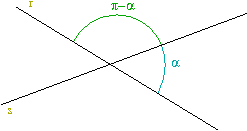
Bajo este criterio podemos identificar a la pendiente de r como m1 y la pendiente s como m2
Ahora utilizaremos la formula para obtener la tangente de el angulo entre 2 rectas

donde para obtener el valor del angulo solo tendríamos que sacar el arco tangente del valor obtenido.
sustituyendo los valores :
m1 = -2 y m2 = 0.5 quedaría de la siguiente forma.
tan a = 0.5 - (-2) = 2.5 = 2.5 = 1.25
1-[(0.5)(-2)] 1-(-1) 2
y para obtener el angulo
arc tan 1.25 = 51.34°
por lo tanto el angulo formado por las lineas r y s es de 51.34°
Anexo Video
Con toda esta información ya podras resolver el RA 1.2